Introduction

In recent years, the Life Sciences industry has been moving toward outcomes-based approaches due to rising legislative and operational pressures. In this environment, Health Economics Outcomes Research (HEOR) has come to the forefront as a way to measure the effectiveness of therapies and their competitive nature in the market.

One major factor in determining the competitive standing of your product is the price point. Predicting the price change percentages and timings of drugs is important to policy-makers, pharmaceutical companies, and even investment firms, to aid in sound policy and product decisionmaking. If it were possible to use advanced modeling to predict these changes, informed decisions could be made based on these forecasts.

Methodology

To test this theory, Cox Proportional Hazard Models were applied to a set of oncology drugs in the United States to perform predictions. Hazard models are a class of survival models in statistics. Survival models relate the time that passes before an event occurs to one or more variables that may be associated with it. In this case, we are observing the events leading up to a price change in order to predict the timing and percentage of that change.

Using data from First DataBank (2003- 2012), a panel of ex-factory drug prices for drug packs for 18 brand names was examined. The data was converted into survival time data by calculating the time duration between each price change, which results in a total of 200 price increases and 38 censored outcomes.

The hazard models include the FDA approval date for each drug as a variable to answer the following questions: 1) how is the percentage change in price related to the time since the last price change and the time since FDA approval; 2) does the probability of a price change depend on the time since FDA approval?

Results

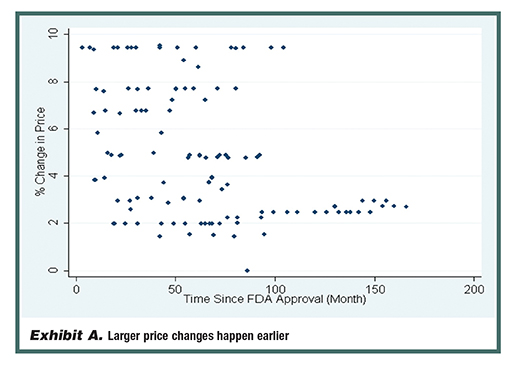
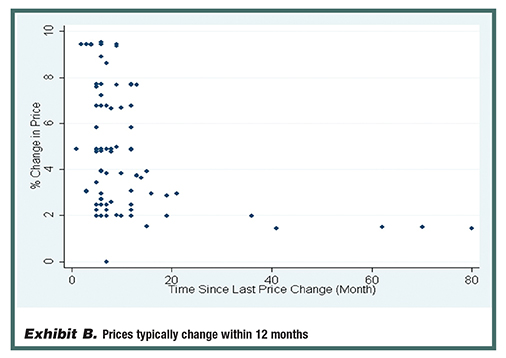
Using the proportional hazard model, the average “event” is a price increase of 5%. For percentage changes in price, for each additional month of constant price, the subsequent price increase drops by 0.08%.

For a second order effect, the negative effect of time since last price change is decreasing. Also, time since FDA approval has a large and significant effect: for each additional month since FDA approval, the subsequent price increase drops by 0.03%.

The average duration between events is 8.8 months. The Cox model shows that for each additional month since FDA approval, the “risk” of a price increase increases by 0.7%. Similarly, there is a second order effect showing this risk diminishing over time. Exhibits A and B illustrate some of the modeling results in graph form.

This case study suggests that Cox Proportional Hazard Models can be used to predict price change percentages and timing of prescription drugs in the market. This information is extremely valuable to decision-makers in the Life Sciences industry, as it enables more informed insights through predictive modeling and analytics on the lifecycle of a drug.

This is just one example of the many possibilities that exist through HEOR studies that aid in the guidance of new treatments and technologies to better manage the rising costs of healthcare both on a national and global level.

Bruce Wang, PhD, MA
Director
Alliance Life Sciences
Consulting Group

Dr. Wang is the Practice Lead of the Health Economics and Outcomes Research Practice at Alliance. He joined Alliance in 2011, and leads his practice in work across the globe. He brings deep expertise in applied economics with a particular focus on health economic models. He has published papers on cost-effectiveness, methodology, pricing, and policy. Dr. Wang was a Senior Fellow in the Pharmaceutical Outcomes Research & Policy Program at the University of Washington. Prior to that, he was an Economic Strategist at Goldman Sachs in New York. He earned his PhD and MA in Economics from the University of Washington and his BA from Columbia University.