Issue:October 2019
ON-BODY DELIVERY SYSTEMS - Analysis & Simulation of Injection Volume Accuracy
INTRODUCTION
In the past several years, in parallel with the increasing development of new molecules, there has been a steadily rising attention among the world’s largest pharma companies to subcutaneous drug delivery devices that can help patients safely self-adhere to their therapy plans.
Of particular interest is replacing legacy autoinjectors with wearable, prefilled on-body delivery systems (OBDS), which represent a revolution in the field of drug delivery. Ease of use and disposability are key factors that are convincing even more players in the market to invest in the development of such devices.
Despite the fact these on-body devices are delivering a subcutaneous bolus to the patient, the accuracy and delivery rate of the drug volume are two of the major performance requirements the system must fulfill.
While injection volume and rate accuracy may be specified for a generic system, the ability of this new wearable system to accurately deliver “labelled” quantity at the desired delivery rate or within the desired time can significantly change the system architecture. Baseline for delivery accuracy inputs typically comes from three primary sources:
Market-Driven: understand similar combination systems (predicate devices) already present on the market or approved by regulatory bodies and their variances
Therapy-Driven: understand the allowable variance from a physiological perspective
Standards-Driven: understand the allowable variance guided by the chosen applicable standards
It is therefore essential to fully define the system needs specific to these inputs from an early development stage, when most of the strategic decisions affecting product development are made. In this review, we will explore key design considerations that impact the volume or dose accuracy.
CONSTRAINTS GIVEN BY NORMATIVE & PRODUCT STANDARDS
Although the adherence to product standards is not mandatory, the development of drug delivery systems (Pen Injectors, Auto Injectors, OBDS, Infusion Volumetric Pumps) is usually driven by the following set of standards:
– ISO11608-1:2014 Needle-based injection systems for medical use – Requirements and test methods — Part 1: Needle-based injection systems
– United States Pharmacopeia USP <905> Uniformity of Dosage Units
– IEC60601-2-24:2012 Medical electrical equipment – Part 2-24: Particular requirements for the basic safety and essential performance of infusion pumps and controllers
– ISO11608-6 (DRAFT under development – stage 30) Needle-based injection systems for medical use – Part 6: On-body delivery systems. This last is a new part (still under evaluation) for the OBDS that refers to Part 1 and is related to Injection Volume Accuracy
Each of these standards establishes clear requirements (depending on the device classification) and test methodologies to assess the capability of a system to accurately deliver the prescribed volume to the user or patient.
DIFFERENCES BETWEEN BOLUS & MULTI-DOSE AUTO INJECTORS
When it comes to dose accuracy, single-dose OBDS are in general, asked to deliver “at least” the value that is declared on the product label, while reusable multidose autoinjectors will generally guarantee a min-MAX accuracy for each single delivered dose.
Technically speaking, for an OBDS that aims to deliver the entire content of the primary container, the variability of the volume injected mainly depends on its geometric characteristics and on air trapped inside the primary container. For reusable autoinjectors, other factors like priming, ability to accurately control the primary container stopper movement, and system volumetric compliance all contribute to the overall system performance.
Hereafter, a more complete evaluation of the Injection Volume Accuracy tailored on OBDS is reported to show through a simplified case study, the effects given by both air trapped and hold-up volume of the primary container
VARIABLES & PARAMETERS AFFECTING DOSE ACCURACY
In general, the dose accuracy or injection volume accuracy for systems aimed to deliver the full dose of the primary container can be calculated according to the following equation:
Equation 1.
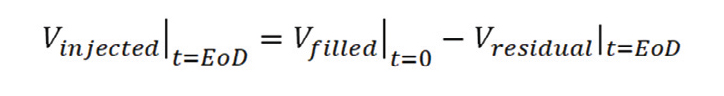
where:
Vinjected | t=EoD represents the volume of drug delivered to the patient, once the injection has been completed (EoD = End Of Dose or Injection).
Vfilled | t=0 represents the volume of drug inside the primary container. This value is established by requirement and only affected by the natural variance of the fill/finish process.
Vresidual | t=EoD represents the volume of drug not delivered to the patient during the injection but that remains/accumulates in the drug delivery system once the injection is completed.
This last parameter is particularly interesting because it is mainly affected by:
– Geometric dimensional variability of the fluid path,
caused by the natural manufacturing tolerances of the individual components part of it (e.g., tubing, needles, cannulas, manifolds, etc)
– Geometric dimensional variability of the part of the primary container between the septum and the stopper (typically the cartridge/PFS shoulder), so-called “container hold-up” volume
– The presence and the volume of the air bubble trapped in the primary container during the fill/finish process.
The air bubble, in fact, plays a major role in the calculation of the injection volume accuracy. In the two extreme cases, it can be acknowledged that:
If the primary container doesn’t contain any air (but only drug) or it is oriented in a way that the air is immediately delivered as part of the drug (as can happen during a priming process), at the end of injection, both the fluid path and the primary container volume will contain only the drug. This residual volume of drug, not delivered to the patient and defined as overall “Hold-Up Volume,” should be taken into consideration and compensated for by over-filling. This mitigation guarantees to avoid systematic under-doses, but at the same time increases the drug-related cost.
Under this condition, the amount of drug that the system can deliver to the patient represents the Minimum Possible Dose:
If the primary container contains a significant air bubble or it is oriented to let the air stay in the system (adherent to the stopper), at the end of injection, both the fluid path and the primary container hold-up volume will contain a percentage of air that depends upon the relative ratio within the overall system dead volume. If the volume of the air trapped is nominally greater than the overall system hold-up volume, all the content of the primary container is delivered to the patient. Considering that the primary container needs to be overfilled to compensate for the hold-up volume, this second condition represents the Maximum Possible Dose that the system can deliver to a patient.
To give a rough idea of the typical size of the air bubble trapped in cartridges according to a standard fill/finish process, it is reasonable to consider the stopper positioned at a distance of 0.4/0.7 mm from the drug level, having therefore a volume of air into the primary container of about 45-80 μl (for a 3 ml, 12 mm ID primary container). Lower values can be achieved with vacuum stoppering technologies that allow minimized volume of air trapped during the sealing of the primary container after filling.
These numbers are typical for cartridges with standard stoppers. In prefilled syringes (PFS) the “hold-up volume” is significantly smaller, reaching values in the range of a few microliters.
It is possible to numerically model the previously listed variables and quantify their effect on the overall volume injection accuracy. The numerical simulations obtained computing all the inputs and variables involved can be either used to guide the design process of the system or to verify the compliance of an existing system with the given requirements of injection volume accuracy.
CASE STUDY: MODELLING & CALCULATION METHODOLOGY FOR WEARABLE OBDS
Hereafter, the main outcome of a numerical simulation of injection volume accuracy exercised on a wearable patch injector or OBDS is reported. The simulation was planned and executed to guide the design process of the entire system and verify the compliance to a given requirement of injection volume accuracy.
Simplifying, the object of the simulation (therefore the core of an OBDS) can be represented by the system in Figure 1, where an ISO13926- compliant 3.0 ml (12 mm ID) glass cartridge is connected to a 25 G needle (so-called “Septum Needle”), to a 0.5 mm ID soft tube and to a 27 G needle (so-called “Skin Needle”). The other end of the system is delimited by the primary container stopper.
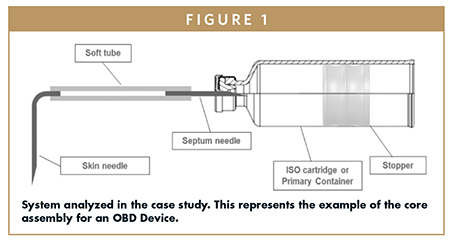
The main assumption behind the numerical evaluation of the dose accuracy is that the system is equipped with enough energy to guarantee that the primary container stopper can reach the mechanical End-of-Travel (e.g., cartridge shoulder) considering all the tolerances affecting the system.
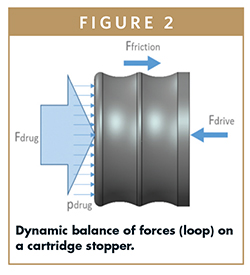
To do that, it is mandatory to design the subsystem responsible to move the stopper (extrusion or drive subsystem) computing all the forces that it must overcome to deliver a given value of drug in a given time interval. This is particularly important if the system (or, as often happens, the platform) is designated to inject multiple drugs with a wide range of viscosities.
Equation 2.
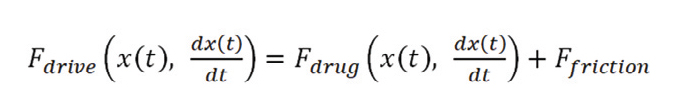
The resolution of the time-dependent differential equation allows one to properly compute for:
– all the pressure drops/losses inside the fluid path
– the friction (static and dynamic) offered by the sliding of the stopper along the primary container barrel
– the mechanical characteristics of the drive subsystem, as a function of the energy source it uses (e.g., mechanical spring, electromechanical actuator, gas cartridge, etc).
This process allows for the design of systems where systematic under-doses due to incomplete travel of the primary container stopper never happen; and for those cases caused by single fault events, monitoring functions shall be in any case added to the device as risk control measures.
At this point, the injection volume accuracy can be calculated by the resolution of Equation 1. In order to have a more realistic representation of the variability of the results, a Monte Carlo statistical approach can be used.
With this approach, it is possible to generate a set of results (for the volume of drug delivered to the patient) corresponding to a random variation of the input variables within their allowed tolerance ranges. This enables a statistical distribution from which statistical indicators (average and variance) can be inferred (see equation 3 below).
Equation 3.

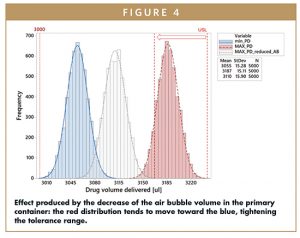
The plot in Figure 3 shows the result of a simulation (run on a sample size of 5000 simulated devices ) for Vinjected. The blue distribution represents the minimum Possible Dose (min_PD) that can be delivered to the patient. The left tail is positioned just at the right of the amount to be delivered by requirement (3 ml) with an average slightly moved to the right to include the natural variability of the hold-up volume and of the filling process. In the event that an air bubble greater than or equal to the hold-up volume is trapped, in the worst case, the quantity of drug delivered can be represented by the red distribution. The distance that characterizes this distribution from the previous represents the offset generated by the overfilling. The bigger the hold-up volume, the greater the overfilling required is to meet the dose requirement in case all the air is immediately injected to the patient at the start of the therapy. On the other hand, in case the air is able to expel all the liquid from the primary container and the fluid path, a larger dose results delivered to the patient.
The difference between the right tail of the Maximum Possible Dose (MAX_PD) and the left tail of the minimum Possible Dose defines the tolerance range (USL-LSL) for the injection volume accuracy.
By reducing the volume of the air bubble (eg, by use of vacuum stoppering technologies in fill/finish) it is possible to observe a movement of the Maximum Possible Dose distribution toward the Minimum Possible Dose distribution, because the probability of having liquid into the fluid path increases. When VAirBubble→0, the Maximum Possible Dose Distribution tends to overlap to the Minimum Possible Dose distribution, narrowing the tolerance window for the injection volume accuracy.
This dual representation of the aforementioned distributions can also be associated with the device orientation that cannot be modelled and randomized as can the other contributors to the equations. In the first case (blue distribution), the orientation allows the air to exit the system immediately after the fluid path opening. At the other extreme (red distribution), the orientation will play the opposite role: the air stays inside the system until the end of delivery, causing the extrusion of all of the drug initially contained in the primary container.
Once the effect of the air bubble is captured and its volumetric value established/optimized, the numerical model can be used to optimize the system geometries to best match the target accuracy window, taking into account the typical tolerances of the components’ manufacturing processes.
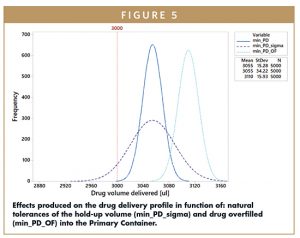
The plot shown in Figure 5 qualitatively highlights how the geometric tolerances of the fluid path components and over-filling are modifying the volume of Vinjected.
CONCLUSIONS
The aforementioned methodology demonstrates that it is possible to have a realistic prediction of the injection volume accuracy of a drug delivery system, even in an early stage of product development, when only a high-level product architecture is available.
The statistical numerical model developed, which includes the realistic variation of all the variables involved, allows one to:
– Evaluate the performance of a system against a given requirement and hence change or reject it
– Support the design process to optimize the system to reach the desired performance level
– Through sensitivity analyses, identify the most critical parameters that may call for particular attention during manufacturing
– Accurately estimate the system dead volume and its natural variance, which is directly linked to the volume of drug to be over-filled and therefore directly linked to cost
The aforementioned approach is particularly important for systems and platforms that have an intrinsic and non-negligible hold-up volume. For systems that use cartridges or custom solutions for the primary container, the presence of the air trapped is significantly increasing the variability of the actual delivery profiles, hence demanding a wider tolerance window for the delivery.
PFS (prefilled syringes) are less affected by the presence of the air bubble. Considering the almost negligible hold-up volume, virtually all of the drug is delivered in a single dose; this leads to narrower tolerance intervals for injection volume accuracy and reduces the need and the extent of the over-filling.
To view this issue and all back issues online, please visit www.drug-dev.com.

Christian Riva is a Senior Systems Engineer at Flex, a global company providing design, engineering, manufacturing, supply chain, and logistics to companies across industries, including medical devices. He manages the development lifecycle for drug delivery, on-body delivery systems, wound management, and wearable diagnostics. He began working at Flex in 2010 as a Mechanical Design Engineer for In-Vitro Diagnostic Medical Devices, and later, electromechanical Drug Delivery Devices. He earned his MS in Mechanical Engineering from Politecnico di Milano Tech University in Milan, Italy.
Total Page Views: 8067