DEVICE DESIGN - Autoinjector Design Adjustment to Control Needle Insertion & Initial Injection Speed – Could This Positively Impact Drug Delivery?

SELF-ADMINISTRATION & BIOLOGICS HAVE BECOME KEY DYNAMICS IN THE PARENTERAL SEGMENT

The rising prevalence of chronic diseases, requiring frequent medication, is very often combining with the growing trend of self-administration (eg, in-home care settings). In order to fit to this new mode of administration, and bring ease of use to the patients while limiting the risks, these drugs are preferably delivered in the subcutaneous tissue, being a very good match for the use of autoinjector devices.

In parallel, a majority of the new drugs in the pipelines of pharmaceutical companies are so-called “biologics.” These new biologic drugs, such as monoclonal antibodies (mAbs), are very good candidates for the treatment of the aforementioned chronic diseases.  Antibodies are natural molecules of the immune system, and these molecules can be modified by biotechnological companies to obtain “biologic drugs.” Biologics have become a significant driver for new treatments, with more than 2,700 remedies in development as of mid-2017, which is three times higher than in 2013.¹ Within the top 100 products, biotechnology drugs represent 49% in 2017, and are projected to maintain a dominant position in the pharmaceutical market over the coming years as they are widely used to treat auto-immune, or inflammatory diseases as Rheumatoid Arthritis, Multiple Sclerosis, Psoriasis Arthritis, etc.²

Biological drugs are very often needed in high concentration: this can be driven by the nature of the molecule, composition of the final drug, and by the effort to decrease the frequency of treatment for the patient. Their viscosity increases as power law of the antibody concentration. Thus, to be injected, these molecules need to be diluted, which leads to higher injection volumes, and lower (but still high) viscosity. As a result, larger dose drug deliveries are a growing segment, with volume shifting toward 2 ml.

CHALLENGES OF BIOLOGICS ADMINISTRATION WITH AUTOINJECTOR DEVICES

Injecting larger volume, with high viscosity, through thinner needles, requires high injection force. It is also observed that a larger dose of viscous formulation leads to higher skin back forces. Usage of higher energy level to deliver viscous formulations could result in higher shocks on the syringe, especially at the end of syringe insertion and start of syringe emptying, and consequently increases the risk of glass syringe breakage.

Controlling the needle insertion speed can reduce the shock on the prefilled syringe. Lowering this shock will reduce the risk of glass breakage, and will allow a smooth transition to syringe emptying. Also, it was demonstrated that pressure waves generated from device actuation could lead to glass breakage.³ Reducing the syringe speed contributes to the reduction of the pressure waves, reducing then the risk of glass breakage. The mechanism of glass breakage has been thoroughly looked at, understood, and described in the literature.^4-7

It is well known that glass has no macroscopic plasticity. It will break before the elastic limit when subjected to tensile stress. These are fragile materials. The mechanism of glass breakage is a crack propagation starting from stress concentrators. The most important stress concentrators are associated to the following:

– glass development, such as bubbles or solid inclusions

– glass forming

– impact during transfers, handling

In the case a mechanical load is applied, glass breakage might occur, originating from one of these stress concentrators. As expressed previously, glass breakage can be simply expressed as: GLASS BREAKAGE OCCURS WHEN LOAD x CRITICALITY ≥ TOUGHNESS.²

In order to prevent breakage, it is then required to minimize loads or flaws generation especially during handling and transport. It is generally admitted that every glass surface contains flaws. In consequence, injection device mechanism should then minimize the loads or chocks on the syringe during use.

OBJECTIVES

The objectives of this study include the following:

– to develop a calculation method for needle insertion speed and energy level transmitted to the syringe

– to use our calculation method to improve injection devices allowing smooth transition between needle insertion and syringe emptying, especially for large dose, viscous formulations, and thin needles

– to validate our calculation method and our improved injection device by experimental measurements

CALCULATION METHOD

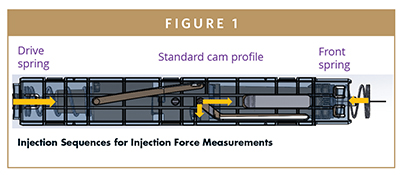
Our autoinjector contains the syringe with the needle and the following specific mechanical components:

– Drive Spring is connected to plunger pusher, which is connected to the needle plunger pusher

– Needle pusher is connected to syringe housing

– Syringe housing contains the syringe

– Front spring is connected to the front housing and the syringe housing

– Front housing is pressed by the patient for activation

Just after activation, the spring force is pushing a specific part, the needle pusher. This needle pusher is following a cam. This cam is an adjustable path allowing needle insertion at a controlled speed. First, theoretical calculation approach is given for a 2.25-ml syringe. Needle insertion speed, and energy transmitted to the syringe are calculated. In case of stiff spring usage, it is possible to lower the speed and energy by:

– A specific cam profile for needle insertion

– Using a counter spring back force

In our method, as highlighted hereafter, we take into account specific cam profile, drive spring, and front spring back force to calculate insertion speed and energy.

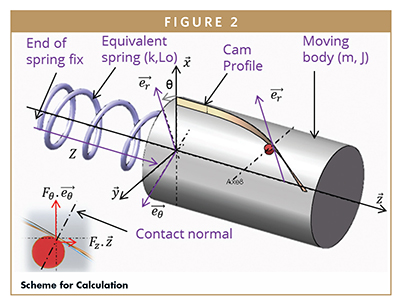
The first part of the calculation aims at predicting needle speed during insertion phase. After this phase, the spring pushes on the plunger rod and injection begins. Calculations are based on following equations: Newton’s second law of motion (fundamental principle of dynamics) say that the sum of the forces F> on an object is equal to the mass m of this object multiplied by the acceleration of this object, as shown on Figure 1.

With: J, inertia of moving body including parts in rotation; R, radius of the cam shaft; m, mass of moving body including parts in translation; k, stiffness of the equivalent spring; l, distance from equilibria position l = (L0 – z); FZ, axial contact force on the cam; FO, radial contact force on the cam.

Assumption: friction not taken into account. The equation of the cam gives:

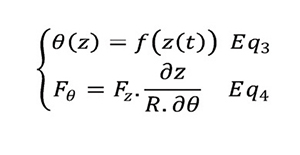
Error! Reference source not found. presents the cam profile chosen for proof of concept.

By combining the 3 previous equations:

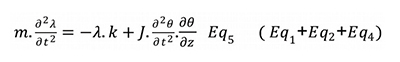
The final differential equation is:

Solving this differential equation by numerical calculation allows access to axial position and axial speed at each step of needle insertion stroke. Furthermore, Energy generated by the cam (Eccame) can be calculated as the following:

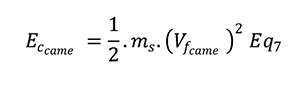DEVICE IMPROVEMENT

Based on our calculation method, we evaluate the influence of cam parameter on linear speed and energy, and we propose an improved configuration.

Click image to enlarge

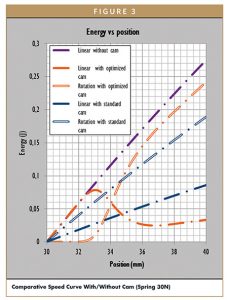
Figure 3 shows that the device with cam shows a theoretical reduction of needle speed from 4,4 m/s to 1,6 m/s at the end of insertion phase. Link to speed, we can calculate the kinetic energy of each systems as show in Figure 3. The reduction on linear speed is about 64%. The energy of the impact transmitted to the syringe is the linear kinetic energy at the end of the insertion, because the syringe is stopped just before starting injection. This kinetic energy takes the speed into account the square of linear speed.

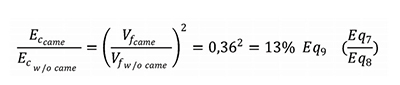
The ratio of linear speed with came on linear speed without cam is 36%. In theory, thanks to the cam, impact energy on the syringe is reduced by 87% (1%). This is a significant shock energy reduction that will reduce the risk of glass breakage especially when very stiff springs are used. Stiff springs are more and more used in autoinjectors to deliver large volume of viscous formulations, through very thin needles.

EXPERIMENTAL TESTS: OPTIMIZED SAFELIA AUTOINJECTOR FOR VISCOUS DRUGS

Tests and comparison with theoretical calculation. Tested sample:

– 2.25 ml, 27G ½” TW

– Drive Spring characteristics 30N

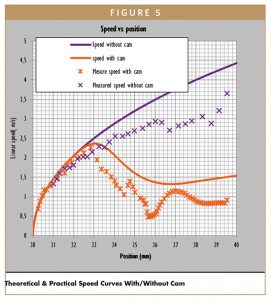
Needle insertion speed was measured with a high-speed camera:

– Without cam: up to 3,5 m/s, after 10-mm stroke

– With cam: only 0,9 m/s , after 10-mm stroke

Click image to enlarge

The measured reduction of linear speed is about 75% against 64% in theoretical calculation (Figure 5).

Click image to enlarge

Compared to the theoretical calculation, needle insertion speed is decreased due to friction of prototype parts, not considered in the math modeling. Without cam, jetting is observed at start of injection. This jetting can be explained by the high impact energy transmitted by the plunger rod to the plunger stopper at start of injection, once needle is inserted. With cam, jetting is not observed at start of injection. This can be explained by the lower impact energy transmitted by the plunger rod to the plunger stopper at start of injection.

REFERENCES

1. Opportunities and Challenges in Biologic Drug Delivery, Michael D. Hooven, American Pharmaceutical Review. https://www.americanpharmaceuticalreview.com/Featured-Articles/345540-Opportunities-and-Challenges-in-Biologic-Drug-Delivery/
2. EvaluatePharma^®, World Preview 2018, Outlook to 2024.
3. Pressure and strain waves in Pre-Filled syringes during autoinjector activation – Jean-Christophe Veilleux1 (Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA, USA), Julian Jazayery (AMGEN, Thousand Oaks, CA, USA), Bruce Eu (Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA, USA) and Joseph E. Shepher (AMGEN, Thousand Oaks, CA, USA), 2018-10 PDA Orlando AMGEN CALTECH oral presentation.
4. Why do Pharmaceutical Glass Containers Break: The Underestimated Power of Strength Testing andFractography, Dr. Dan Haines ( Scientific Advisor for SCHOTT pharma), Dr. Florian Maurer (Senior Scientist for Strength and Fractography at SCHOTT), Dr. Uwe Rothhaar( Director of SCHOTT pharma).
5. Fractography of Ceramics and Glasses, NIST, Special Publication 960-16 (2007), Quinn, G.D.
6. Fracture Analysis, a Basic Tool to Solve Breakage Issues, Technical Information Paper, Toshihiko Ono (Corning Japan K. K., Shizuoka Technical Center) and R. A. Allaire (Corning Incorporated, Science and Technology).
7. Défaillance de casse : l’expertise fractographique Cathie COLIN, Jean-Louis HEITZ, CRITT Matériaux Alsace.

 To view this issue and all back issues online, please visit www.drug-dev.com.

Pascal Dugand is Technology Product Manager at Nemera. He is an experienced medical device developer engineer specialized in the development of parenteral drug delivery devices since 1990. He developed for Nemera its own IP products, including Safe’n’Sound safety device and Safelia auoinjector as well as working on several customer injectable product developments.

Thomas Megard is a Design Engineer, Abylssen for Nemera. He graduated as a Mechanical Engineer from Arts & Métiers in Cluny, France. He started to work as consultant for Abylsen since 2015. In 2017, he started as Design Engineer consultant at Nemera.

Séverine Duband is Global Category Manager at Nemera. She has more than 10 years of marketing experience with key competencies, including strategic planning, NPD launches, project management, and team leadership in an international environment. At Nemera, she particularly focuses on the range of proprietary products, including the Safelia autoinjector device.