CLINICAL TRIALS - Considering Recurrent Events in Clinical Trials Statistical Analysis

INTRODUCTION

Many chronic diseases are characterized by non-fatal recur­rent events. Examples of such include asthma attacks in asthma, epileptic seizures in epilepsy, and hospitalizations for worsening condition in heart failure. Typically, in clinical trials for heart fail­ure, composite outcomes (eg, heart failure hospitalization or car­diovascular death) are adopted as the primary endpoint and then analyzed as a time-to-first-event analysis using the Cox propor­tional-hazards model. These composite outcomes combine fatal and non-fatal events, thereby providing more comprehensive in­formation about the impact of the treatments compared. Com­bining multiple endpoints into one composite outcome also increases the event rate and avoids the multiplicity issues sur­rounding the analysis of multiple endpoints. However, composite outcomes that only consider the first event are suboptimal for a chronic disease such as heart failure, which is characterized by recurrent heart failure hospitalizations, since repeat events within individuals are ignored in analyzes. Recurrent hospitalizations are an indication of worsening condition, so analyzing all these re­peat events within individuals is more representative of disease progression. Furthermore, recurrent hospitalizations are distress­ing for patients and thus outcomes that consider all these events more accurately estimate the effect of treatment on the true bur­den of disease. If we consider the CHARM-Preserved trial, we can examine the impact of analyzing only the time-to-first event, ig­noring repeat hospitalizations.¹

THE CHARM-PRESERVED TRIAL AS A CASE IN POINT

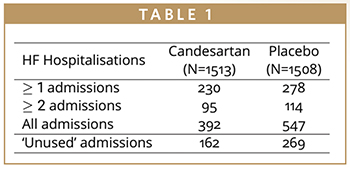
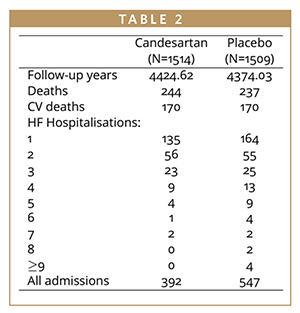
There were 508 patients presenting with at least one heart failure (HF) hospitalization and 209 of these presenting with two or more (Table 1). Patients presented with a total of 939 HF hos­pitalizations, meaning that a time-to-first-event analysis throws away 431 hospitalizations. This is data that is relevant to patients and costly to collect, it shouldn’t just be ignored. The effect of treatment on these non-fatal, recurrent events is important to quantify, but there is controversy as to which statistical methods of analysis are the most appropriate.² Time-to-first-event analysis of composite endpoints remain the gold standard in many indi­cations as the statistical approaches are well established, and there is substantial experience in regulatory assessment. There is notably less regulatory experience for recurrent event endpoints, and the statistical approaches are more complex, but it is impor­tant to consider these methodologies because of the many ad­vantages they present.

Methods for analyzing recurrent events are well developed and can be split into two broad categories: time-to-event ap­proaches and methods based on event rates. Time-to-event methodologies include the Wei-Lin-Weissfeld (WLW), the Prentice-Williams-Peterson (PWP), and the Andersen-Gill. Methods based on event rates discussed here are the Poisson and the negative binomial.

THE WLW MODEL (WEI-LIN-WEISSFELD)

The WLW model examines the cumulative time from ran­domization to K ordered events considering each event in turn as the outcome in a sequence of applications of the Cox propor­tional-hazards model.³ The distinctive feature of the WLW model is that each individual’s time at risk for events (ie, first, second, third event, etc) is considered to start at randomization, so full randomized treatment groups are compared. Thus, in the case of heart failure hospitalizations, time-to-first hospitalization would be analyzed for all randomized patients and an estimated hazard ratio and associated p-value obtained. Then the total time from randomization to second hospitalization would be analyzed sep­arately, again including everyone randomized, even if they hadn’t yet had a first hospitalization, giving a second estimated hazard ratio and associated p-value. Analysis continues in this manner giving K distinct estimated treatment effects for each ordered hos­pitalization, which can be considered in isolation, or these hazard ratios can be combined using weights to give an “average effect.” The advantages of the WLW model are that it preserves random­ization, and it is semi-parametric meaning that there is no as­sumption on the baseline hazard. The disadvantages include issues surrounding the interpretation of the estimated hazard ra­tios. The treatment effect for the second hospitalization, for ex­ample, includes the effect on the first. If a large treatment affect is observed for the first hospitalization, this will have impact on the treatment effect for subsequent events. It is also difficult to in­terpret global effects if the estimated hazard ratios are combined. This methodology also still doesn’t allow analysis of all hospitalizations. Because there are fewer higher order events, analysis must be restricted to a K subset of all hospitalizations. If we con­sider the CHARM-Preserved data, for example, we see that it may only be sensible to consider the first three or four hospitalizations for analysis. So those patients who have five or more hospitaliza­tions will still have some of their events ignored.

THE PWP MODEL (PRENTICE-WILLIAMS-PETERSON)

The PWP model is similar to the WLW, but rather than con­sidering total time to each ordered event, gap times (ie, the times between consecutive events) are considered with conditional risk sets.⁴ Analysis continues in the same manner; however, and distinct hazard ratios are estimated with associated p-values for K gap times. These can once again be combined using appropriate weights and an average global treatment effect obtained. The PWP model presents with many of the same advantages and disadvantages as the WLW model, the main difference being that conditional risk sets in the PWP model better reflect the true dis­ease progression, but do not maintain randomization like the WLW model.

THE ANDERSEN-GILL MODEL

The Andersen-Gill is an extension of the Cox proportional-hazards model, which analyzes gap times.⁵ In the Cox propor­tional-hazards model, each individual’s time to event contributes independently to the partial likelihood, but in the Andersen-Gill model, it is each gap time that contributes independently giving a hazard ratio-like intensity ratio for the treatment effect. Hospi­talizations within individuals are likely to be related to each other with some patients being inherently more/less frail than others, subsequently presenting with increased/ fewer hospitalizations respectively, mean­ing that heterogeneity is often present in the data. The independence assumption ignores this heterogeneity, meaning that analysis can result in standard errors that are too small with corresponding confi­dence intervals that are too narrow, p-val­ues that are too optimistic, and an increased in the Type I error rate. Robust standard errors must be used to accom­modate overdispersion when adopting the Andersen-Gill methodology.⁶ Advantages of the Andersen-Gill model include the fact that it is a semi-parametric approach, and it can analyze all hospitalizations for all in­dividuals. A disadvantage of this method­ology, however, is that it assumes a common baseline hazard for all of the gap times, which may not be true in practice.

ANALYSIS BASED ON EVENT RATES: POISSON & NEGATIVE BINOMIAL DISTRIBUTIONS

Methods based on event rates include the Poisson and negative binomial distri­butions. The Poisson model is a very sim­ple model that considers the total number of events divided by the total follow-up in each group, giving a rate ratio for recur­rent events. This distribution assumes that the underlying event rate is the same across all subjects (and follows a Poisson process) and assumes independence of events, which as has already been dis­cussed, is not a sensible assumption in the case of HF hospitalizations. An alternative approach is to use the negative binomial distribution, which naturally induces an as­sociation between repeat events within in­dividuals through a random effect term, which is assumed to follow a gamma dis­tribution. The negative-binomial assumes individual-specific Poisson event rates con­ditional on a random effect for each pa­tient’s true underlying rate. The negative binomial distribution is easy to implement and does not require complex data files. The resulting estimated rate ratio is also easy to interpret and can comfortably be communicated to non-statistical audi­ences. This methodology, however, comes with a strong distributional assumption for the underlying event process: event rates within individuals are assumed to follow a Poisson process with a constant event rate.

CONSIDERATIONS OF STATISTICAL METHODOLOGY FOR RECURRENT HEART FAILURE HOSPITALIZATIONS

So, which statistical methodology should be used in the analysis of recurrent HF hospitalizations? There are of course many statistical considerations that must be addressed when answering this ques­tion. Would it be preferable to use a mod­eling framework that is semi-parametric over fully parametric? What assumption do we want for the event rate? Constant, time-varying, or leave it completely un­specified? And what should be done to handle the over-dispersion that is often present in this recurrent HF hospitalization data? Often, I believe too much emphasis is placed on these statistical considera­tions, when in fact, I would prefer to see the most appropriate methodology being used to answer the question of interest. Many of these methodologies answer slightly different questions. Perhaps we are interested in the effect of treatment on times to particular events. Maybe we are interested in the effect of intervention on subsequent events among those who had a preceding event. Or we could be inter­ested in the effect of treatment on rates of events. All too often in the analysis of re­current events I see the question being driven by the chosen analysis method. Surely, it’s time to turn this around and use the methodology that best answers the question of interest.

ELEVATED RISK OF CARDIOVASCULAR DEATH: HOW TO ANALYZE USING COMPOSITES

Another key characteristic of heart failure is that an increase in HF hospital­izations is associated with a worsening condition and a subsequent elevated risk of cardiovascular (CV) death, meaning that subjects may die during follow-up. Consequently, any censoring due to CV death is not independent of the recurrent event process. A comparison of heart fail­ure hospitalization rates, between treat­ment groups, can be confounded by this competing risk of death and ignoring the dependent censoring can result in bias in estimated treatment effects. Therefore, any analysis of recurrent events must take into consideration informative censoring that may be present.

One simple strategy for incorporating CV death into analysis of recurrent heart failure hospitalizations is to consider this outcome as an additional event in the re­current event process. That is, one consid­ers a composite of recurrent heart failure hospitalizations and CV death. This up­dated recurrent event process can then be analyzed using all standard recurrent event techniques, and the subsequent es­timated treatment effect that is obtained is an intensity/rate ratio for the composite of repeat heart failure hospitalizations and death. Note that any death that occurs during a heart failure hospitalization would be treated as a single event. This methodology has received positive reac­tion from the regulators and was adopted as the primary outcome in the PARAGON-HF trial.⁷ Regulators seem to like this out­come as it isn’t too far away from the current status-quo; they are used to seeing composite endpoints, and this is an exten­sion of the current gold standard method­ology. But this approach isn’t without its disadvantages. This composite endpoint is composed of many more recurrent HF hospitalizations than CV deaths, meaning that the estimated treatment effect is going to be dominated by the effect of treatment on these non-fatal events. A marginal treatment effect in CV death could be masked by a large treatment effect on HF hospitalizations, and thus it is crucial that any such composite endpoint analysis is also presented with corresponding analy­sis of the component parts and careful at­tention is paid to attributing common treatment effects to each of the different types of event.

THE GHOSH & LIN METHOD

The Ghosh and Lin non-parametric analysis of heart failure hospitalizations takes mortality into account while also ad­justing for different follow-up times and multiple hospitalizations per patient.⁸ This method considers the marginal expected number of recurrent heart failure hospital­izations up to some particular timepoint, t, acknowledging the fact that death is a ter­minal event after which no further recur­rent hospitalizations can be experienced. This means that although a patient stays in the risk set beyond time to death, their associated recurrent hospitalization count stays constant, fixed at whatever value it was just prior to death. The stochastic structure of the recurrent hospitalizations process is left completely unspecified and there are no assumptions regarding the dependence between the recurrent hospi­talizations and death. The mean frequency function is defined as the marginal ex­pected number of recurrent heart failure hospitalizations up to some timepoint, t, acknowledging that no further recurrences occur after death.

JOINT MODELING TECHNIQUES

An alternative approach is the use of joint modeling techniques to obtain esti­mates of treatment effects on heart failure hospitalization rates while allowing for in­formative censoring.⁹ Joint modeling tech­niques are appropriate when analyzing rates of recurrent events whilst allowing for association with a potentially informative dropout time, or when each of the out­comes is of scientific importance to the in­vestigators and the dependence between the two processes needs to be accounted for. One approach to joint modeling is random effects models, which assume that the recurrent hospitalizations and time-to-death are conditionally independent given a latent variable. Models of this kind are intuitively appealing as they can give a tangible interpretation that an individual’s independent frailty term measures their underlying, unobserved severity of illness, which proportionately affects both their heart failure hospitalization rate and their time-to-death (or CV death). Joint models allow distinct treatment effects to be esti­mated for each of the processes, while tak­ing account of the association between the two. Joint frailty models can also be para­metric or semi-parametric, allowing flexi­bility in the underlying assumptions. One of the disadvantages of joint modeling methodologies is that two co-primary pri­mary endpoints must be specified in the statistical analysis plan. Regulatory experi­ence in this area suggests that preference is given to analysis that consider only one primary endpoint that incorporates both non-fatal and fatal events (such as the composite outcome of recurrent HF hospi­talizations and CV death), rather than two co-primary endpoints that must be consid­ered together. Additionally, if it were re­quired to power studies on CV death as well as HF hospitalizations, very large sample sizes would be needed as treat­ment effects on CV death are typically marginal, compared with larger treatment effects for HF hospitalizations.

SUMMARY

The world of recurrent events in HF studies is complex, and there is no obvious right answer. This is perhaps why it is so interesting! There is also still a significant amount of work to be done in this area. The methodologies considered here either assumed a constant HF hospitalization rate or left the underlying rate completely unspecified. But what if we wanted to ex­plicitly model a non- constant rate? Clini­cians believe that hospitalizations may cluster and that the event rate may in­crease just prior to death. It may be desir­able to develop methodology that captures these features of the data so that these as­pects can be quantified. All these analysis have also assumed that events are instantaneous, which is obviously not true for the case of hospitalizations. It may be that treatment not only affects if a patient is hospitalized, but also how long they must subsequently stay in the hospital. Multi-state models would allow us to model the effect of treatment on transitions into and out of the hospital, as well as transitions to death. I look for­ward to seeing how this field of statistics develops in the future.

REFERENCES

1. Yusuf S, Pfeffer MA, Swedberg K, Granger CB, Held P, McMurray JJV, Michelson EL, Olofsson B, Östergren J. Effects of candesartan in patients with chronic heart failure and preserved left-ventricular ejection fraction: the CHARM-Preserved Trial. The Lancet. 2003;362:777-781.
2. Rogers JK, Pocock SJ, McMurray JJ, Granger CB, Michelson EL, Östergren J, Pfeffer MA, Solomon SD, Swedberg K, Yusuf S. Analysing recurrent hospitalizations in heart failure: a review of statistical methodology, with application to CHARM-Preserved. Euro J Heart Fail. 2014;16(1):33-40.
3. Wei LJ, Lin DY, Weissfeld L. Regression analysis of multivariate incomplete failure time data by modelling marginal dis­tributions. J Amer Statist Assoc. 1989;84(408):1065-1073.
4. Prentice RL, Williams BJ, Peterson AV. On the regression analysis of multivariate failure time data. Biometrika. 1981;68(2):373-379.
5. Andersen PK, Gill RD. Cox’s regression model for counting processes: a large sample study. Ann Statist. 1982;10(4):1100-1120.
6. Lin DY, Wei LJ. The robust Inference for the Cox Proportional-hazards model. J Amer Statist Assoc. 1989;84:1074-1078.
7. Solomon SD, McMurray JJV, Anand IS, Ge J, Lam CSP, Maggioni AP, Martinez F, Packer M, Pfeffer MA, Pieske B, Redfield MM, Rouleau JL, et al. For the PARAGON-HF Investigators and Committees. Angiotensin–Neprilysin Inhibition in heart failure with preserved ejection fraction. NEJM. 2019;381:1609-1620.
8. Ghosh D, Lin DY. Nonparametric analysis of recurrent events and death. Biometrics. 2000; 56(2):554-562.
9. Rogers JK, Yaroshinsky A, Pocock SJ, Stokar D, Pogoda J. Analysis of recurrent events with an associated informative dropout time: application of the joint frailty model. Statist Med. 2016;35(13):2195-2205.

Jennifer Rogers is Head of Statistical Research and Consultancy for the CRO PHASTAR, and has broad portfolio of achievement, particularly in the development of clinical trial methodologies. She provides leadership and advice to statistical consultancy activities, and directs the statistical research strategy helping the company stay at the cutting edge of new methodological advances. She joined in 2019, following a move from the University of Oxford, where she was Director of Statistical Consultancy Services and an Associate Professor in the Department of Statistics. She had previously worked as a post-Doctoral Research Fellow in the Department of Statistics funded by the National Institute of Health Research. She is Vice President for External Affairs at the Royal Statistical Society and has made numerous appearances on UK TV and radio.